Text and Image Compression
C++ program to compress text and images, inspired by lack of storage on my phone
Technologies Used: C++, Data structures, Encoding, compression, decompression
The Idea
I kept on running out of storage on my phone and became curious about how compression works
Development
1. Researching compression
I knew that compression was a method of encoding from larger to smaller, but was not sure how this was done. When trying create a compression mapping myself,
I realized that my approach would be ambiguous to decompress. Would the bits 1010101101 be decoded into
10 10101 101 or 1010 10 110 1 ? These would result in different
decompressed results.
I then found Huffman encoding. Huffman encoding removes ambiguity with prefix codes where the code that one character is mapped to will not be the prefix
of the code another character is mapped to. If "a" is 11 , then there will not be any character whose code start with
11 .
2. Building a Prefix-code Tree
I built the prefix code tree by determining the frequency of each character (for text) and pixel value (for images), and creating a Huffman tree from it. This was done using a min-priority queue that created a specific tree where the leaves were the characters and the branches represented the encodings. Traveling left was a '0', traveling right was a '1'.
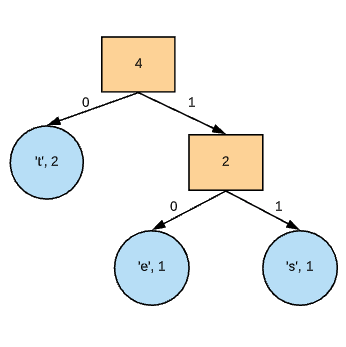
Image of prefix-code tree for "test".
Following this tree, the letters of "test" will be encoded as follows:
- "t" - 0
- "e" - 10
- "s" - 11
Because the tree is generated from a min-heap (by letter frequency), it takes into account more commonly used letters and those appear closer to the root, which is why 't' has a shorter code. This allows for frequently used letters to take up less space (1-bit in this case).
3. Encoding the Tree
The letters are encoded, but their meaning still needed to be communicated with the program performing the decoding. This could have been Development
by encoding the character-to-coding table, but it could also be done by directly encoding the tree. This is especially easy because each node of a Huffman
tree will have a valence of 2, allowing the tree to be easily decoded recursively. This also prevents the need for a delimeter between header and main body
within the compressed file.
From the "test" encoding example, the encoded header appears as follows:
01t01e1s
It can be interpreted as follows: The path to the leaf node -> leaf node specified by a 1 -> character
(The characters will be encoded into binary)
4. Decoding the Tree
After I created the compressed file, I also wanted to be able to decompress it. To do so, I had to recreate the header from the compressed file, create the same Huffman tree from that header, and then use that tree to decode the compressed body.
5. Testing!
Dictionary of words (lowercase)
letter | code
' | 11110011100
q | 11110011101
j | 1111001111
x | 111100110
z | 11110010
w | 0011110
k | 0011111
v | 1111000
f | 001110
y | 100010
b | 100011
h | 111101
p | 00100
m | 00101
g | 00110
u | 10000
d | 11000
c | 11001
l | 11111
o | 0110
t | 0111
n | 1001
r | 1010
a | 1011
s | 1101
i | 1110
e | 000
\n| 010
Encodings of the letters within the dictionary
0001e001p1m01g01f01w1k01\n01o1t00001u01y1b1n01r1a0001d1c1s01i0001v01z01x001'1q1j1h1l
Compressed Header (characters are in ascii for demonstration)
--------------------- Compression Stats ---------------------
Uncompressed Bits: 6355472
Compressed Bits: 3388691
Compression %: 46.6807
Compressed Header (characters are in ascii for demonstration)
Something that was important for me to understand was that any encodings larger than 8 bits were less efficient than ASCII. But even though there are a few of those in this example, the most frequently used characters are less than 8 bits, allowing for a decrease in space consumed.
Image
To apply the same algorithm to the image, I would be compressing the pixel intensity values which - just like characters - are also 0-255. This meant I just needed to add code to read in the image pixels, and send those pixels into my compression program.

Image I am compressing (379x248)
1 126 1 22 1 106 1 36 2 106 1 85 3 75 1 187 1 106 1 215 2 35 1 106 1 59 3 36 1 36 1 187 1 22 1 75 1 89 1 59 1 35 2 89 1 35 1 35 2 89 1 187 1 35 2 11 2 25 1 11 3 35 1 135 1 161 1 110 1 133 1 125 1 184 1 110 1 161 1 184 2 44 1 184 1 24 1 57 1 161 1 59 1 138 2 98 1 44 2 59 1 119 1 101 2 89 1 75 1 158 1 108 4 72 1 1 3 35 1 35 2 11 1 72 3 11 11 2 1 2 2 35 1 25 1 72 1 11 1 60 1 60 1 11 2 158 1 194 5 108 1 158 0 17 1 187 1 22 1 59 1 50 2 85 6 85 1 63 1 85 2 239 1 106 1 138 1 187 2 106 1 63 1 63 1 138 1 89 2 187 1 22 4 187 4 59 7 35 5 126 1 2 1 3 1 126 1 72 1 25 1 1 3 72 1 59 2 179 1 125 1 110 1 104 1 224 1 110 4 214 1 184 4 107 1 180 1 107 1 24 1 224 2 147 1 87 1 139 1 110 3 98 1 85 4 59 1 101 2 62 2 75 2 158 1 194 3 1 1 25 1 35 1 60 1 20 1 1 5 2 1 25 1 2 1 35 1 25 1 20 1 25 4 158 1 60 1 158 1 194 1 0 1 126 1 50 1 85 2 106 2 138 2 36 1 85 2 106 2 36 1 63 1 75 1 22 3 36 4 138 1 44 1 59 1 22 1 101 1 187 1 89 2 101 1 187 1 35 2 50 1 75 2 45 1 50 1 75 4 25 1 50 1 59 2 44 1 180 2 58 1 224 2 180 1 110 1 184 1
Decompressed pixel intensity (1st row)
--------------------- Compression Stats ---------------------
Uncompressed Bits: 751936
Compressed Bits: 304477
Compression %: 59.5076
Compression Stats
Something that was important for me to understand was that any encodings larger than 8 bits were less efficient than ASCII. But even though there are a few of those in this example, the most frequently used characters are less than 8 bits, allowing for a decrease in space consumed.
Areas of further research
- Looking into how other compression alogithms work - specifically Lempel–Ziv–Welch (LZW)
- Looking at improvements to Huffman Coding by implementing statistics about natural letter distributions in the compressed language
victortaksheyev@gmail.com