WFF Algorithm

Algorithm for restoring parentheses in sentential logic sentences to turn them into well-formed formulas (WFFs)

Key concepts/tech used: recursion, combinatorics, python, mathematical modeling
Under the guidance of Dr. Jesse Fitts

The Idea

Meaningful logical sentences are called well-formed formulas (WFFs). The definition of a WFF is recursive:

1. Atomic sentences are WFFs
2. If $\phi $ is a WFF, so is $ \lnot \phi $
3. If $\phi $ and $\psi $ are WFFs, so are $\phi \land \psi $, $\phi \lor \psi $, $\phi \rightarrow \psi $, $\phi \leftrightarrow \psi $
4. Nothing else is a WFF

WFF	Not WFF
$A$	$AB$
$(A\lor B)$	$A( \lor B)$
$(A\lor B) \rightarrow (\lnot C)$	$A( \lor \land \lnot B )$

While there are infinite ways to add parentheses to WFFs for them to remain WFFs, there are finite ways to restore parentheses to sentences to turn them into WFFs. The number of ways to restore parenthesis is a function of the number of operators within the sentence being restored. The following is demonstrated below:

Connectives	Ways of Restoring Parenths	Demo
0	1	$(A)$
1	1	$(A \lor B)$
2	2	$(A \lor B) \lor C$ $A \lor (B \lor C)$
...	...	...
$n$	$W(0) = 1$ $W(n) = \sum\limits_{k=1}^{n-1} W(k)W(n-1-k)$ for $n>0$	...

*For readability, I excluded parentheses around atomics

My goal was to create an algorithm that would take a sentential logic sentence as input and ouput all possible well-formed formulas

Algorithm for 2-place connectives

For each connective in the sentence, I am treating it as the "major connective", creating a left and right side with respect to it, then recursively performing the same process on the left and right sides until I reach an atomic. Once I reach the atomic, I return it, adding parentheses to the result.

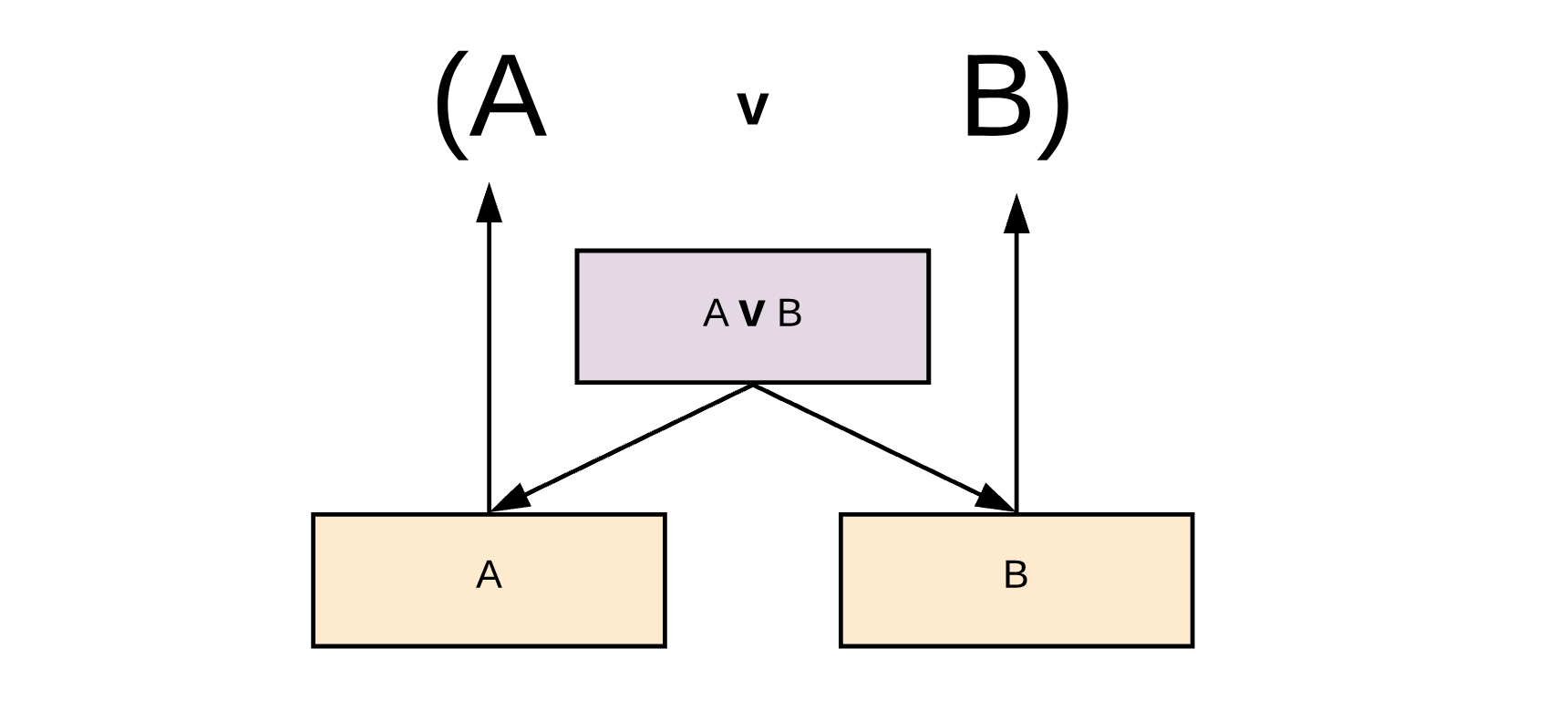
Demonstration of how a sentence is decomposed into a left and right until atomics are reached. The result is returned and concatenated with parentheses and operator.

While recursion is used to decompose and restore parentheses, it is insufficient. An iterative element is used to loop through each connective to treat it as the "major connective".

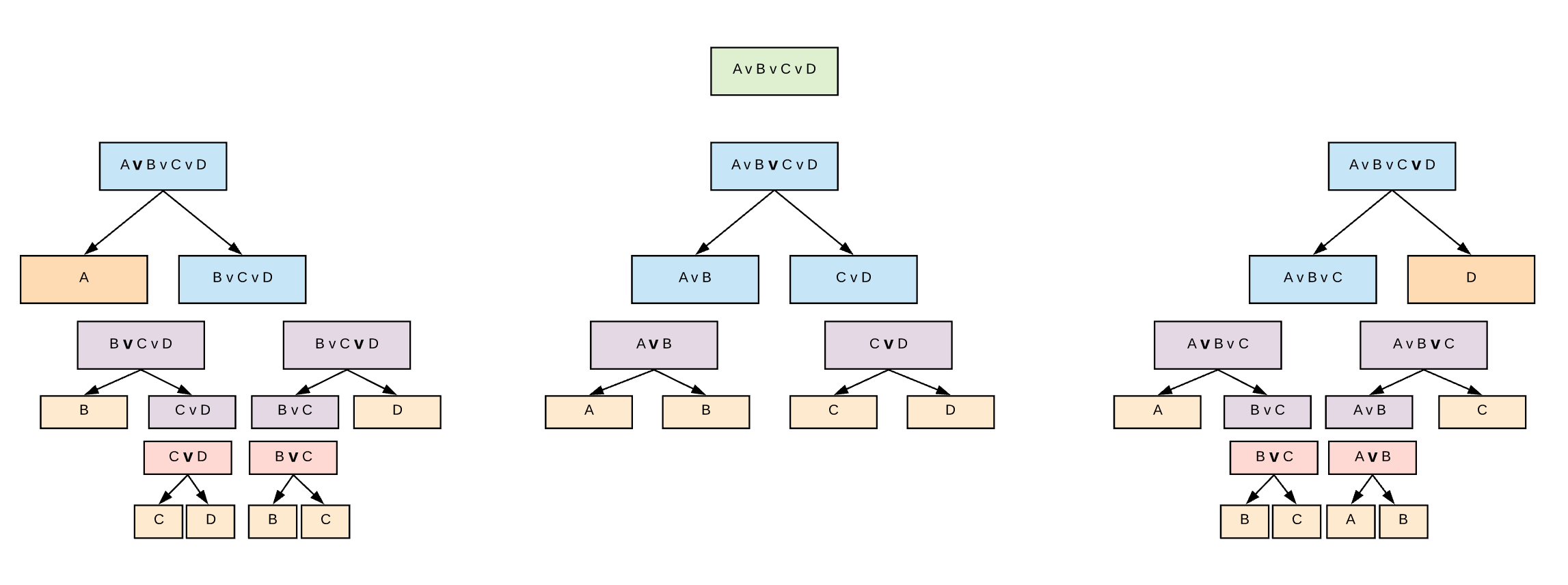
Together, they are able to cycle through all of the operators, decomposing each into a left and right and reconstructing them as well-formed formulas.

def rec(wff):
    ind = []                                        
    if len(wff) == 1:
        yield wff
        return 
    else:
        for i in range(numConnectives(wff)):        
            opIndex = findConnective(wff, ind)      
            right   = createRight(wff, opIndex)     
            left    = createLeft(wff, opIndex)      
            for left_subexpr in rec(left):
                for right_subexpr in rec(right):
                    yield "(" + left_subexpr + ")" + wff[opIndex] + "(" + right_subexpr + ")"

Main recursive algorithm to handle two-place operators written in python

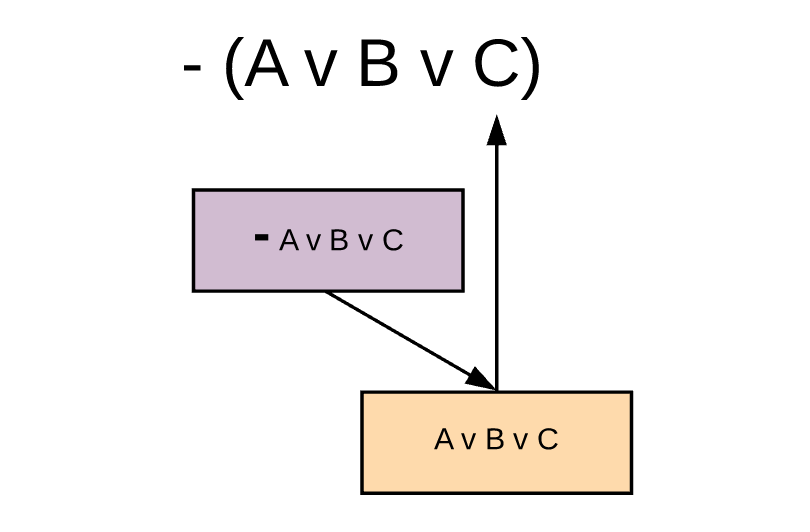
Adding in the 1-place connective

The one-place operator only governs over what's immediately to the right of it. Because of this, there is no longer a left side and right side. There is only a right side

            def rec(wff):
                ind = []                                        
                if len(wff) == 1 and wff not in one_place_conn:
                    yield wff
                    return
                if len(wff) == 2 and one_place_conn in wff and (wff[0] and wff[1] not in one_place_conn):
                    yield "(" + wff + ")"
                    return 
                else:
                    for i in range(numConnectives(numOnePlaceConns(wff), numTwoPlaceConns(wff))):        
                        opIndex = findConnective(wff, ind)      
                        right   = createRight(wff, opIndex)     
                        left    = createLeft(wff, opIndex)     
                        if (wff[opIndex] == one_place_conn):
                            if (len(left) > 0):
                                for left_subexpr in rec(left):
                                    for right_subexpr in rec(right):
                                        yield "(" + left_subexpr + wff[opIndex] + right_subexpr + ")"
                            else:
                                if (len(right)>1):
                                    for right_subexpr in rec(right):
                                        yield "(" + wff[opIndex] + right_subexpr + ")"
                                else:
                                    break
                        else:
                            for left_subexpr in rec(left):
                                for right_subexpr in rec(right):
                                    yield "(" + left_subexpr + wff[opIndex] + right_subexpr + ")"

Addition of the 1-place operator case into the recursive algorithm

Since the 1-place connective case is just a part of a more general algorithm, the algorithm continues on the right side of the one-place connective - regardless if it encounters one or two-place connectives.

Testing on my homework

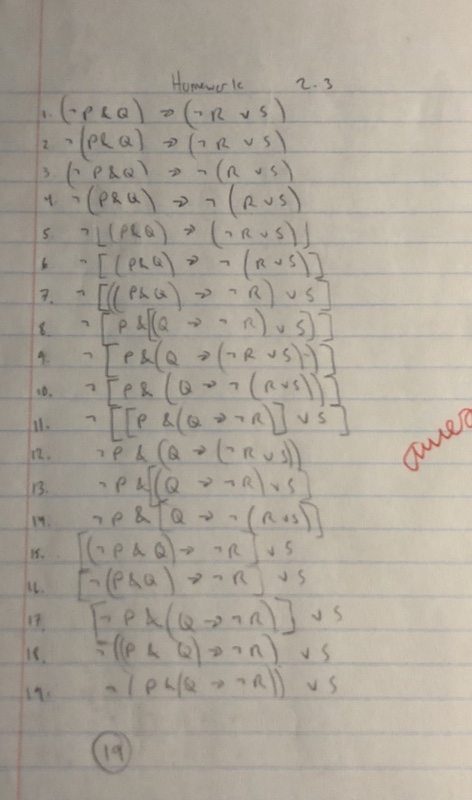
Enter SL sentence: -P&Q>-RvS
All possible well-formed formulas:
1 (-(P&(Q>(-(RvS)))))
2 (-(P&(Q>((-R)vS))))
3 (-(P&((Q>(-R))vS)))
4 (-((P&Q)>(-(RvS))))
5 (-((P&Q)>((-R)vS)))
6 (-((P&(Q>(-R)))vS))
7 (-(((P&Q)>(-R))vS))
8 ((-P)&(Q>(-(RvS))))
9 ((-P)&(Q>((-R)vS)))
10 ((-P)&((Q>(-R))vS))
11 ((-(P&Q))>(-(RvS)))
12 ((-(P&Q))>((-R)vS))
13 (((-P)&Q)>(-(RvS)))
14 (((-P)&Q)>((-R)vS))
15 ((-(P&(Q>(-R))))vS)
16 ((-((P&Q)>(-R)))vS)
17 (((-P)&(Q>(-R)))vS)
18 (((-(P&Q))>(-R))vS)
19 ((((-P)&Q)>(-R))vS)

While not in the same order, the algorithm produced the correct result.

Findings

WFF Possibilities From 2-place Operators

Operators	WFFs Possible
0	1
1	1
2	2
3	5
4	14
5	42
6	132
7	429
8	1430
9	4862
10	16796
11	58786
12	208012
...	...

After looking up this sequence, I found that it was called the Catalan Numbers. These numbers come up in counting problems such as "the number of possible Binary Search Trees with n keys" or "the number of ways an $n$-gon can be divided into $n-2$ traingles". From this project, I found out that they also apply to the number of ways parentheses can be restored to logical sentences with 2-place connectives.

Further Research

Make algorithm more efficient, using dynamic programming
Figure out the mathematical relationship between $n$ and $m$-place connectives.